03: Reasoning: How LLMs Solve Complex Reasoning Tasks
-
Tart: A plug-and-play Transformer module for task-agnostic reasoning (Jun 2023, added 6/25/23)
Certified Reasoning with Language Models (Jun 2023, added 6/11/23)
Tree of Thoughts: Deliberate Problem Solving with Large Language Models (May 2023, added 5/23/23)
Reasoning with Language Model Prompting: A Survey (Dec 2022)
Language Models Are Greedy Reasoners: A Systematic Formal Analysis of Chain-of-thought (Jan 2023)
Solving Quantitative Reasoning Problems with Language Models (Jul 2022)
Why Does ChatGPT Fall Short in Answering Questions Faithfully? (Apr 2023, added 4/25/23)
Is ChatGPT a Good Recommender? A Preliminary Study (Apr 2023)
Are Emergent Abilities of Large Language Models a Mirage? (Apr 2023, added 5/1/23)
LLMs Still Can't Plan; Can LRMs? A Preliminary Evaluation of OpenAI's o1 on PlanBench
Large Language Models as General Pattern Machines (Jul 2023, added 7/18/23)
(link)
Cool paper that shows that LLMs are surprisingly good as pattern recognition machines: i.e., give them some kind of sequence, ask them to complete it, and they’ll get it right pretty often. This must be some basic, foundational way in which they work, because it shows up without any specific training.
For sequence transformation, the paper uses the Abstract Reasoning Corpus, a general AI benchmark that contains collections of 2D grids with patterns that evoke abstract concepts (e.g., infilling, counting, and rotating shapes). Each problem provides a small number of input-output examples, followed by test input(s) for which the objective is to predict the corresponding output. Two important findings:
The experiments indicate that LLMs in-context prompted in the style of ASCII art can correctly predict solutions for up to 85 (out of 800) problems – exceeding some of the best performing methods to date, without additional model training or fine-tuning.
Surprisingly, if you replace this ASCII art with randomly sampled tokens, it still works well. These results suggest an intriguing insight: that LLMs may exhibit more general capabilities of representing and extrapolating symbolic patterns, invariant to the specific tokens involved.
Here are the results for sequence transformation: the best previous method uses a hand-crafted domain specific language to solve the problems. Just with in-context learning, GPT 3.5 gets close. (However, this is still only a solve rate of 10%! While this benchmark is hard, it’s not shooting the lights out. Then again, this isn’t GPT-4 either.) Also a cool insight: “w/ random A” means that you map the input tokens from ASCII art into random other tokens (even unrelated Chinese letters) - and the LLM can still solve 50% of the problems as compared to previously.
The paper also looks at sequence completion and sequence improvement (like giving the LLM a sine wave and seeing if it can continue it correctly). Those results are similar. The paper then studies how well these capabilities can be used to create steering commands for robots (which are just sequences of commands, and what we’re doing here is completing and improving sequences, so it should work). Less interesting for our purposes here but there seems to be something there.
Tart: A plug-and-play Transformer module for task-agnostic reasoning (Jun 2023, added 6/25/23)
Here is a fundamental conundrum of today’s LLMs: it’s very clear that they come out-of-the-box as too “generalized”, meaning, they’re not particularly good at specialized tasks you want them to do. But:
you can give them lots of in-context examples, in which case the base model remains very generally useful because you can just change your prompt to a new set of examples - but you can’t use a lot of training examples (because the prompt window is too small)
or you can fine-tune them, in which case you can use lots of examples - but you lose the generality of the model because now you’ve fine-tuned it and can’t just change the prompt anymore
or some other method like using adapters (an extension of an LLM with a bunch of more hidden layers that you fine-tune directly), but those all have just variations of the same problems above.
Why is any of this even necessary? Because LLMs are just not very good at classification problems. So this paper’s idea is the following: why don’t we train another model that is just very good at generic logistic regression (classification) problems? Here is a nice illustration of the 4 methods: in-context learning just uses prompts and doesn’t change anything else; fine-tuning changes all the weights; adapters modify just the weights of a module at the end; and TART (this paper) adds a reasoning module at the end that is just good at logistic regression.
The particular problem that the paper studies here is a sort of binary classification problem: for example, input = “The movie is good”, output = “positive” (sentiment). In other words, we want to put a label on the input.
First, the paper studies what LLMs are actually good and bad at. Take the classification problem from above: it could be that the LLM fails at representations - meaning, it fails to properly pick up on the objects/entities it needs to distinguish in order to reason about them. Or it could be that the LLM fails at reasoning - meaning, it understands the entities/objects in the input, but it can’t put them together in just the right way. So here are some neat insights:
First, they train a “linear probe” for an open-source LLM. This “linear probe” means you take the embeddings from some intermediate layer, and you try to map those into an output directly. This is as if we opened up the LLM, and we extract what it was “thinking” at any intermediate layer. The idea is that if the linear probe already gets you a good answer, it cannot be a problem with “representation” - because if we simply take the “representations” at some intermediate layer, and we train our own simple linear classifier, we find a good answer.
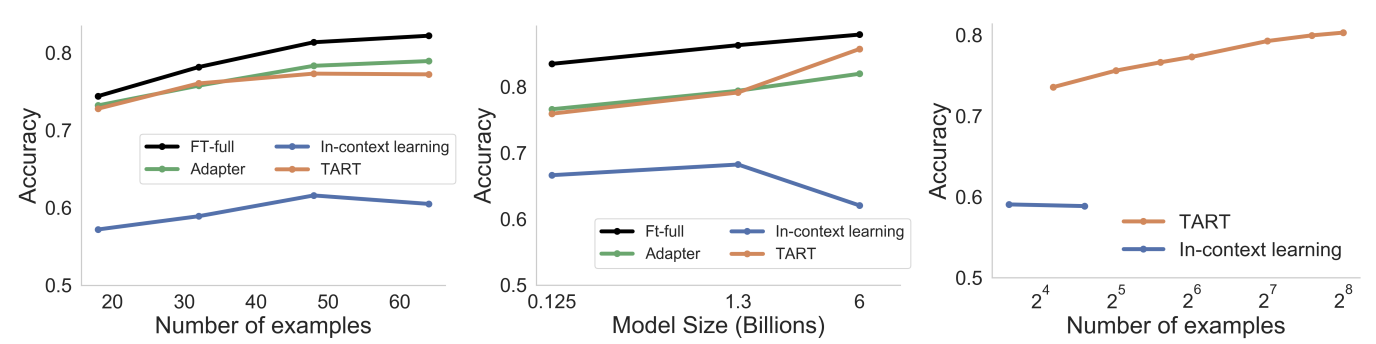
Look at the chart below: even just training our own linear probe vastly increases our accuracy! That means that the LLM “had the answer on its tongue”, but because it is too dumb to execute a simple regression, it couldn’t extract it from its own representations. But if we fine-tune the LLM, we can easily get it there as well.
Second, they run the chart above, but they look at various different examples of fine-tuning the LLM for different problems. If we take the difference between the blue and the red line as the “reasoning gap”, and the difference between red and black as the “representation gap”, and we try a number of different problem fine-tunings, we get the chart below: basically, in almost all problems that we fine-tune on, we always get most of the gains coming from improvements in reasoning, not in representation. The LLM very rarely has a problem of “seeing” - really only of “thinking”.
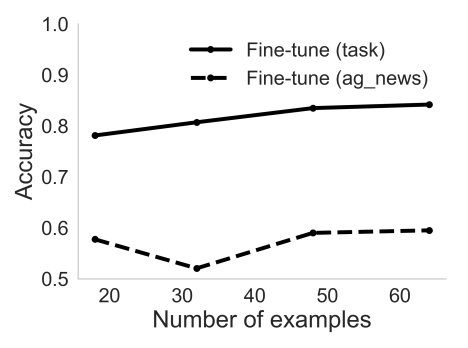
So why don’t we just fine-tune all the time? Because of the issue in the chart below: when we fine-tune for the task “task”, and then we fine-tune on the task “ag_news”, the performance on the original task goes into the toilet. The LLM just can’t “generalize to both”.
So what does the paper propose? A deceptively simple idea: apparently, using that linear probe (again, a really simple classifier that we trained separately) worked really well. But it’s of course not generic. So why not just train an LLM on a generic logistic regression problem? That’s what they do. Here is now the paper's main idea: give the LLM a "reasoner"! This "reasoner" should be generically usable, and essentially help the LLM do classification tasks. The simple idea: train another transformer - but train it simply on completely generic logistic regression output! How do we do that? We simply pick a list of 30 words, and we create a synthetic dataset such that we can map any occurrence of these 30 words either into the label "positive" or "negative". Like: "sports love null car ... cat: positive, null love null car ... null: negative, sports null hat null ... cat : positive". We can do that through a deterministic algorithm (i.e., we purposefully build in a "pattern" that can get discovered if you run a logistic regression on this synthetic input data). Then we actually feed a lot of those examples into a GPT-2 transformer that we train to detect the right label for a particular input of words. So that simple transformer simply learns what a basic logistic regression looks like.
Once you have that “reasoning” transformer, you simply put the embeddings from the actual LLM’s last layer directly in there, and the final output comes out of the reasoning transformer. This works really well, and most importantly, it’s totally generic, you don’t need to re-train the thing on a new problem. It’s just generically good at logistic regression-type answers.
From Word Models to World Models: Translating from Natural Language to the Probabilistic Language of Thought (Jun 2023, added 6/24/23)
(link)
This is a powerful paper with a simple idea: to get an LLM to reason in much more well-defined ways, use it to write a probabilistic language program! We’ve had programming languages for that for a while, like Prolog - you set up the logic problem in well-defined ways, and the program gets executed to run inference. But those programs are really, really hard to set up because the translation from natural language into a precise logic language is so ambiguous and hard. Well, creating code is exactly what LLMs are good at, so just use an LLM for that. So: describe to the LLM the problem, ask it to write the probabilistic language program, run the program (and feed the results back to iterate further). The probabilistic language is good at supporting coherent belief updating and inferences over beliefs.
It is quite straightforward: Church is a well-known probabilistic language. The chart below gives two examples for how we first write rules in Church that define the “world” we’re going to reason about. We put those into the LLM prompt. We then give some observations as natural language, and write their corresponding Church translations, also in the prompt. That’s the few-shot learning part. Then we can use the LLM to add additional conditions, and query the world. The LLM translates those into Church, and our Church interpreter will run it all.
Church works as follows: Inference is based on drawing samples from the prior over world states described by the generative model, and rejecting those that fail satisfy the constraints of any observation conditions. The samples that remain constitute a posterior sample over possible worlds consistent with the observed information, sufficient to answer the queries under consideration in the language discourse.
Here is another example, top to bottom. The world model (A) is written by us: here, we say that each player in the world has a variable called strength, and it’s a random Gaussian variable. We say each player has a variable called laziness, and it’s random too. We then define how to calculate the strength of a team: it’s the sum of all players’ strength (unless a coin flip on laziness knocks it down by a factor of 2 for a player). Finally, we define who wins when two teams compete. In (B), we give the LLM some few-shot examples to be able to translate natural language into Church - for example, we condition the world on the fact that the team of players John and Mary won against the team of players Tom and Sue. Finally, in (C), we give the LLM sentences to translate into Church, which we then add to Church. When we ask a question, you can see how Church actually runs a Monte Carlo-type simulation by sampling from the allowed universe of inference-derived facts.
Finally, even cooler: they hook up a physics simulation engine to Church. The function simulate-physics actually runs a real simulation which then sends the calculations back into the samples of Church. Nothing else changes, but now you can even adhere to physical laws in an additional engine that puts constraints onto the reasoning process.
Certified Reasoning with Language Models (Jun 2023, added 6/11/23)
(link)
This paper presents a simple but compelling idea: we know that LLMs are (surprisingly?) able to reason quite well, i.e., to go from one logical step to the next, in order to prove an argument. But there is no guarantee in the LLM itself that the inference it decides to make is formally correct. So this paper does two things:
First, prompt the LLM to turn its input into formally noted logical statements, of the type of format that can be fed into a logical prover engine.
Second, every time the LLM makes an inference step, actually feed that step into the logical prover, and prove formally if it’s correct. If not, halt the process.
See below for an example. The paper just gives the LLM (here, GPT-3.5) a number of few-shot examples like this, and it’s able to follow from there. See how the LLM first “translates” the described context into the formal syntactic structure that will work with the external logic prover:
“Every dog is small” is translated into “Every [[prop:dog]] is [[prop:small]]”. This means the external logic prover will now be able to see both “dog” and “small” as logical propositions (objects it can reason with).
“Every dog is small” is also translated into “[[axiom:(dog ‘x) -> (small ‘x)]]”. This is a preposition from first-order logic: we now have a formal axiom that says “for every x that is a dog, that x is small”, with both “dog” and “small” recognized as formal logic objects.
Now we give the LLM the formalized goal: [[goal:(not (bitter alex))]]. Note that this is not where the external logic prover comes in: it’s still the LLM doing the entire reasoning chain! The only difference is that we ask the LLM to always articulate its reasoning in this formal type of language which we can check externally.
So the LLM starts with “Alex is a vertebrate”. It translates this into [[infer:(vertebrate alex)]]. Ok, that is now where the external logic prover comes in: every time the LLM generates “[[“, the external engine gets fired up and checks if the following statement is true. If it’s false, then the external prover feeds that back to the LLM, for it to continue on another branch. That’s like asking the LLM to write Python and feeding a Python error message back into the prompt.
This is useful stuff: quite obviously, we can now make absolutely sure that an inference chain that the LLM produces is formally verifiable. Not entirely sure how useful this is in real-life applications because formalized logic is quite hard to articulate in the real world, but it’s a thoughtful approach.
Tree of Thoughts: Deliberate Problem Solving with Large Language Models (May 2023, added 5/23/23)
(link)
The paper proposes a new way to reason with LLMs: rather than just asking an LLM for a answer, or asking it to explain its answer (chain-of-thought), or asking it several times for an answer (self-consistency), you ask an LLM to first decompose solving a problem into “thought steps” and then solve each step individually, then arrange all that into a nice little “thought tree”.
Here is an example for how this works: take the Game of 24, where you get 4 numbers, and you have to write an equation that equals 24 (like 4 9 10 13 => (13-9)*(10-4) = 24).
Comparing Machines and Children: Using Developmental Psychology Experiments to Assess the Strengths and Weaknesses of LaMDA Responses (May 2023, added 5/23/23)
This paper runs a bunch of basic child psychology tests on LaMDA (Google’s LLM - a little outdated, this is not their latest LLM). These are tests like “if a car drives behind a curtain, does it still exist”. They convert these classical tests into language, and they also modify them so that the LLM doesn’t just regurgitate the classical results from simply having ingested the original research papers. What emerges is a cool illustration of what LLMs are good at (at least LaMDA - again, kind of an outdated LLM already): a) they’re good at social understanding (probably because they’ve been trained on so much language), b) they’re performing merely at chance in object/action understanding and theory of mind, and c) they’re worse than children at causal reasoning. But most importantly: regardless of the “absolute” level of these scores (10 would be equivalent to human children) - LaMDA just doesn’t learn like a human. These scores should really all be at the same level, if an LLM learned like a human. Instead, they’re all over the place.
Selection-Inference: Exploiting Large Language Models for Interpretable Logical Reasoning (May 2022)
(link)
The paper looks at how good LLMs are at reasoning. It proposes a new prompting mechanism that forces an LLM to break each reasoning step into two: first, selection (which fact in the prompt is going to be used for inference), second, inference (what does the fact imply). It turns out this simple mechanism beats even chain-of-thought prompting.
Existing approaches to teaching LLMs how to reason:
approaches that try to fine-tune LLMs to produce the final answer directly, keeping reasoning implicit
approaches that encourage LLMs to produce reasoning explicitly, but all reasoning steps are produced in one generative step
approaches that use LLMs to produce each reasoning step one at a time.
General insights into reasoning:
In general it was found that the approaches that incorporate explicit reasoning work better than those that only try to predict the final answer
But encouraging the models to produce multiple steps of reasoning in a single generative pass is not enough to make the models use reasoning in a causal manner: the generated reasoning traces often contain unrelated or incorrect steps while still resulting in the correct answer
By using the simple selection-inference framework, the paper gets much better results at logical reasoning questions:
Reasoning with Language Model Prompting: A Survey (Dec 2022)
(link)
The paper looks at how well LLMs are able to perform reasoning.
Some notes on this:
For prompt engineering, single stage means to give one prompt. Multi-stage means you try to elicit step by step questions and answers from the model by running several prompts and modifying the original prompt. Chain-of-thought is still single stage, because it’s just one prompt.
Few-shot prompting performs better in almost all tasks as model scale increases, which can be explained by the fact that LMs with larger model size contain more implicit knowledge for reasoning
Chain-of-thought prompting produces much greater increases, with PaLM-540B showing the greatest improvements
However, when the model scale declines to less than 100B, CoT prompting will yield no performance gain and may even be detrimental. Thus, CoT prompting elicits an emergent ability of model scale, which is defined as abilities of pre-trained LMs which are not present in smaller-scale models but in large-scale models
Pre-training on code branch not only enables the ability of code generation/understanding but may also trigger the reasoning ability with CoT. The exact cause is still elusive, but one theory could be that code is a more reasonable form of text, thinking about procedure-oriented programming is analogous to solving problems step by step, and object-oriented programming is analogous to decomposing complex tasks into simpler ones
Explicit high-quality reasoning rationales contained in the input context are the keys for reasoning with LM prompting. The reasons are not well understood yet.
Language Models Are Greedy Reasoners: A Systematic Formal Analysis of Chain-of-thought (Jan 2023)
(link)
This is a clever paper that tests reasoning and proof construction of LLMs by artificially creating a simple ontology and deriving a simple proof from it, then testing if the LLM can figure that out by itself.
The paper first randomly generates an ontology between 3 and 10 concepts: each ontology is a set of concepts (e.g., mammal, cat, carnivore, etc) and subtype relations between them (e.g., ∀x(cat(x) → carnivore(x))). The ontology also describes properties of concepts (e.g., ∀x(mammal(x) → ¬cold_blooded(x))).
It then generates a proof by randomly picking a node and starting with an axiom, such as cat(billy), and then walking up the ontology tree such as: cat(billy) => carnivore(billy) etc.
It then converts the ontology and the proof into natural language and that becomes the prompt for the model. In half the cases, it makes the proof false on purpose.
It then gives the ontology and proof to the model and asks it to say true/false.
The paper categorizes the reasoning created by the LLM as follows:
Validity: if a proof step is provable from the previous step (e.g., cats are carnivores + carnivores are mammals => cats are mammals)
Atomicity: if a proof step follows from the previous step with exactly one rule application (e.g., Billy is a cat. Billy is a carnivore. <= this is missing an intermediate step even though it’s valid)
Utility: if a proof step is valid, but it doesn’t help with the ultimate proof goal, i.e., is some pointless piece of information (this is called “misleading”)
Several insights from the experiments:
Only the largest model is able to reason
Real-world knowledge helps reasoning: if the ontology reflects the real world (i.e., isn’t just entirely made up), the model does better
Longer proofs are still challenging. The model handles 1- and 3-hop examples quite well but struggles with 5-hop top-down examples, with accuracy falling to chance.
Traversal direction affects reasoning. As the number of hops increases, the model becomes sensitive to the traversal direction of the ontology (top-down vs bottom-up).
Most predicted proof steps are strictly-valid (in the 5-hop experiments with fictional ontology, 93.2% of proof steps are strictly-valid, 2.4% are broadly-valid, and 5.9% are invalid).
LLMs tend to skip steps by producing non-atomic steps, just as humans do when they verbalize their reasoning (in the 5-hop experiments with fictional ontology, 2.4% of proof steps are nonatomic, even though all steps in the few-shot examples are atomic)
Most incorrect proofs contain misleading steps and invalid steps.
For the best-performing models, the main source of reasoning error is from misleading steps, since most predicted steps are strictly-valid and atomic. Once the model goes down the wrong path, it sometimes doesn’t recover. Therefore, it seems that while LLMs are able to produce valid proof steps with high probability, they have difficulty with proof planning/strategizing.
In general, the more time the model spends outside the correct proof path, the less likely it becomes to return to the correct proof.
Towards Reasoning in Large Language Models: A Survey (Dec 2022)
(link)
One Oct 2022 paper claims that LLM are “decent zero-shot reasoners”, another Jun 2022 paper says “LLMs are still far from achieving acceptable performance on common planning/reasoning tasks which pose no issues for humans to do”.
It appears clear that reasoning is absent in smaller language models, but potentially emerges in larger ones (above 100B parameters).
The paper goes through Chain of Thought as one possible way to elicit better reasoning capabilities from an LLM.
Various other papers discuss self-consistency: here, an LLM is used to create several different chains-of-thought to solve the same problem, and then the most consistent answer is picked. (This just means we pick the answer that is yielded by the most independent chains.)
Techniques of “rationale verification” assign a score to each rationale based on various criteria, which can be used to filter out the best rationales.
Finetuning LLMs on training datasets of specific tasks (multitask learning, such as sentiment analysis vs. text summary) improves reasoning capabilities.
Another idea is to first decompose problems, for example through least-to-most prompting, where sub-problems are solved in a specific order.
But, all in all: all these prompting techniques don’t address the underlying reasoning capabilities of the LLM
To improve reasoning, consider:
Lewkowycz et al. (2022) find that LLMs trained on datasets containing scientific and mathematical data can achieve better performance on reasoning tasks like quantitative reasoning problems when using CoT prompting
Anil et al. (2022) study the length generalization abilities of LLMs, i.e., whether LLMs learned with short problem instances can generalize to long ones. If you simply ask an LLM to output intermediate results to a scratchpad and feed them back in, you get a significant improvement in LLMs’ ability to generalize to longer problems, while this phenomenon is not observed in the standard fully supervised finetuning paradigm.
Saparov and He (2022) find that, when using CoT prompts, LLMs are able to produce valid individual proof steps, even when the ontology is fictional or counterfactual. However, they may sometimes choose the wrong steps when multiple options are available, leading to incomplete or incorrect proofs. Moreover, for many reasoning tasks where the performance of standard prompting grows smoothly with model scale, chain of thought prompting can lead to dramatic performance improvement.
Reasons to believe LLMs can reason:
high performance on various tasks requiring reasoning (Suzgun et al., 2022);
the ability to reason step-by-step with chain of thought prompting (Wei et al., 2022b)
the reflection of human-like content effects on reasoning (Dasgupta et al., 2022).
Reasons to believe LLM cannot reason:
LLMs still struggle with tasks that require complex reasoning (Valmeekam et al., 2022; Han et al., 2022; Ruis et al., 2022). If LLMs are really decent reasoners, they should handle tasks that can be simply solved by humans through reasoning;
LLMs make mistakes in their reasoning, as explained above;
The performance of LLMs on downstream tasks has been found to be sensitive to the frequency of certain terms, such as numbers, in the training data (Razeghi et al., 2022; Jung et al., 2022), which would not be expected if the models were solving mathematical problems through reasoning;
Language models have been found to struggle with associating relevant information that they have memorized (Huang et al., 2022c).
Solving Quantitative Reasoning Problems with Language Models (Jul 2022)
(link)
The paper introduces Minerva, a large language model pretrained on general natural language data and further trained on technical content.
Minerva is based on the PaLM general language models that are further trained on a high-quality dataset containing scientific and mathematical data. In particular, we start with 8B, 62B, and 540B parameter pretrained models, and continue training them on our technical content dataset.
The main novelty of this paper is a large training dataset that juxtaposes natural language with the correct use of formal mathematical language, such as equations and diagrams
Training: Our models were trained on a dataset of 38.5B tokens from webpages filtered for mathematical content and from papers submitted to the arXiv preprint server. None of those were part of the original LLM training. In addition, the dataset includes general natural language data, which is the same dataset that was used for pretraining PaLM. (In total, 17.5B tokens from math web pages, plus 21B tokens from arXiv). Our mathematical webpage dataset was constructed by collecting pages that contain mathematical expressions in MathJax format. The pages underwent a cleaning process that removes most HTML tags but preserves mathematical notation, including LATEX symbols and formatting. The result is that mathematical formulae like eπi + 1 = 0 or E = mc2 are presented in full to the model during training.
Other insights from using the model:
We find that we can considerably outperform greedy decoding by sampling k > 1 solutions (with a non-zero temperature) and selecting one using majority voting. This consists of grouping predictions with respect to their final answer and selecting the most common answer.
Log-likelihood is another metric that can be used to rerank samples. We found that majority voting performs significantly better than log-likelihood reranking
Interesting to look at the failures of the model: 41% incorrect reasoning, 35% incorrect calculation, 11% misunderstand question, 13% other.
Another problem: false positives. We can automatically verify the model’s final output, but not its intermediate steps. So the paper manually looks at a sample of proofs and calculates the “false positive” rate: the percent of solutions where the solution was right but the path was wrong. By difficulty level, the false positive rate is:
When examining model solutions, we find that memorization of intermediate facts, such as numerical values of square roots or trigonometric identities, are crucial elements of model solutions. Truly strong performance would combine recall of intermediate facts with genuine solution synthesis.
But overall, we find little evidence that the model’s performance can be attributed to rote memorization.
Why Does ChatGPT Fall Short in Answering Questions Faithfully? (Apr 2023, added 4/25/23)
The paper tests ChatGPT in complex open-domain question answering and tries to figure out how it goes wrong. It runs 200 questions from HotpotQA and BoolQ (question sets based on Wikipedia) through ChatGPT and reviews the results manually, and does the same for 1,000 questions for quantitative evaluation. It then distinguishes 4 criteria:
Comprehension: The model demonstrates proficiency in comprehending the problem, but it exhibits shortcomings when faced with problems containing grammar mistakes or ambiguity.
Example: What is a rare breed of dog that was derived as a variant of Rat Terrier, Shiloh Shepherd dog or American Hairless Terrier? => That comma should be a colon, and the model selects among all three variants instead of just the last two.
Factualness: The model simply holds or cites the wrong facts.
Example: Which canal is longer, New Orleans Outfall Canals or Augusta Canals?
Specificity: Model answers too generally.
Example: What profession do Kçbç Abe and Agatha Christie share? GPT's answer is author, but it should be playwright.
Inference: Model possesses the necessary knowledge to answer a question, but fails to reason with the facts effectively to arrive at the correct answer.
Example: Which is currently more valuable, Temagami-Lorrain Mine or Meadowbank Gold Mine? => GPT knows that Temagami is shut down, but doesn't infer that this means it's less valuable
Here are the results:
Observations:
Most errors are factualness errors
GPT-4 improved on comprehension and specificity, but not very much on factualness
They then dig into what goes wrong when the model makes factualness mistakes:
70% of knowledge-related errors were due to the inability to memorize knowledge (the model can't extract the facts)
15% occurred during the knowledge association process (the model has the facts but can't connect the facts to answering the question)
15% took place during knowledge reasoning (the model has the facts, can connect them, but makes a mistake in reasoning with them).
They look into how you can improve performance in QA tasks, and the table below shows their various approaches.
Summary:
Providing evidence is best. The model actually gets better if you simply point it to the right Wikipedia page. But the more evidence in the prompt, the better.
Providing evidence not only addresses factualness but also significantly mitigates comprehension and specificity errors.
However, inference errors seem to be difficult to improve with evidence.
Is ChatGPT a Good Recommender? A Preliminary Study (Apr 2023)
The paper tests ChatGPT as a general-purpose recommendation model. The idea is powerful: LLMs have way more extensive linguistic and world knowledge than any specialized recommender system, and that could be powerful. Five scenarios: (1) rating prediction, (2) sequential recommendation, (3) direct recommendation, (4) explanation generation, and (5) review summarization.
The test itself is simple and not particularly well-designed: write a prompt for each recommendation task, run it through ChatGPT, evaluate the result.
Rating prediction task: how will a user rate a particular item? Prompt for zero-shot: “How will user rate this product_title: "SHANY Nail Art Set (24 Famous Colors Nail Art Polish, Nail Art Decoration)", and product_category: Beauty?”. Prompt for k-shot: add 5 of these descriptions plus the user’s rating in the prompt.
Sequential recommendation task: what to recommend to the user next? Prompt for zero-shot: “The user has interacted with these 5 items: [list them]. Recommend the next item to interact with.” Prompt for k-shot: add an example sequence.
Direct recommendation task: rank the next best items in order of priority. Prompt for zero-shot: “The user has interacted with these 5 items: [list them]. Of the next 5 items below, rank them best to worst to interact with next.” Prompt for k-shot: add an example ordering.
Explanation generation task. Prompt: “Help user generate a 5.0-star explanation about this [product]”
Review summarization task. Prompt: “Write a short sentence to summarize the following product review from user”
The results are as follows:
Rating prediction: ChatGPT performs better than state-of-the-art on, but only if you give examples in k-shot.
Sequential recommendation: ChatGPT sucks. Not surprising, given that the model gets almost no interesting input data to go on (see the prompts above).
Direct recommendation: Same, it’s bad. Not surprising given the pretty bad prompt.
Review summarization: It performs well, but that’s not surprising given that it’s a language task.
Overall, not an earth-shattering paper given the simplicity of its prompt design.
Are Emergent Abilities of Large Language Models a Mirage? (Apr 2023, added 5/1/23)
This is a great paper that does something very simple: it quite conclusively shows that the phenomenon of “emergent abilities” of LLMs might simply be a measurement mirage. The paper does not say that LLMs don’t get better at all kinds of tasks when they get bigger - it just says that those abilities don’t show up as suddenly as previously described.
The idea is very simple: if you really look at where LLMs in previous papers have shown “emergent abilities” (the model gets very suddenly very useful at a task, when it goes above a particular size), then 92% of the tasks that this happens for are in these two categories:
So it’s a pretty simple insight: it’s quite intuitive that your scoring for extract string matches gets “suddenly” great if you really just measure the non-continuous, discrete, jumpy metric of “output string exactly matches target string! If you measured more continuously, then you might see the LLM’s gradual improvement at the task.
The paper then tests this out, by running a particular task on GPT-3, and just measuring it in different ways. Below is the most important chart: it shows a task that it runs LLMs of different sizes at, and provably the per-token error rate goes down gradually (A). If you then run a metric where an entire sequence of tokens has to be end-to-end correct, then not surprisingly that metric only flips to a good score once the error rate falls below a particular threshold. That creates the “thresholding” emergent ability measurement in C and D. If you just measure the same test more continuously, it just looks continuous (E and F).
Nifty paper, it doesn’t really change anything about how “good” LLMs get when they get bigger, but the “suddenness” of the emergence of these abilities goes away, and that’s good to see.
LLMs Still Can't Plan; Can LRMs? A Preliminary Evaluation of OpenAI's o1 on PlanBench )
(Sep 2024, link)
The paper tests the new OpenAI o1 models on the benchmark PlanBench. It suggests that while 4o can be viewed as an approximate retriever, o1 seems to have been trained as an approximate reasoner.
The benchmark presents problems in “Blocksworld”. Here is an example problem:
I am playing with a set of blocks where I need to arrange the blocks into stacks. Here are the actions I can do: Pick up a block, Unstack a block from on top of another block, Put down a block, Stack a block on top of another block.I have the following restrictions on my actions: I can only pick up or unstack one block at a time. I can only pick up or unstack a block if my hand is empty. (etc.)As initial conditions I have that, the red block is clear, the blue block is clear, the yellow block is clear, the hand is empty, the blue block is on top of the orange block, the red block is on the table, the orange block is on the table and the yellow block is on the table. My goal is to have that the orange block is on top of the blue block.Here is a version of this in PDDL:
(define (domain blocksworld-4ops)(:requirements :strips)(:predicates (clear ?x)(ontable ?x)(handempty)(holding ?x)(on ?x ?y))(:action pick-up:parameters (?ob):precondition (and (clear ?ob) (ontable ?ob) (handempty)):effect (and (holding ?ob) (not (clear ?ob)) (not (ontable ?ob))(not (handempty))))(etc.)
Here is a “mystery” version. This is a clever test because it is extremely unlikely that this weird problem is part of any pretraining with these exact words.
I am playing with a set of objects. Here are the actions I can do: Attack object, Feast object from another object, Succumb object, Overcome object from another object. I have the following restrictions on my actions: To perform Attack action, the following facts need to be true: Province object, Planet object, Harmony.(etc.)
Here is the “randomized mystery” version, it is even more cryptic:
I am playing with a set of objects. Here are the actions I can doJ4gv801gnu2it0yj object_0 object_1. U64y1a9apusmslxb object_0. Kip9uw781pv62umn object_0. Wio5amhq7814n006 object_0 object_1.I have the following restrictions on my actions: To perform j4gv801gnu2it0yj action, the following facts need to be true: tv30k33pzoulql6w object_1, and a46zhwykn6jvbabk object_0.(etc.)
One remarkable insight: the paper tested both natural language prompts and PDDL, and found that vanilla language models perform better when tested on the former. This is interesting because LLMs just don’t need intermediate representations anymore, they can deal just fine with language.
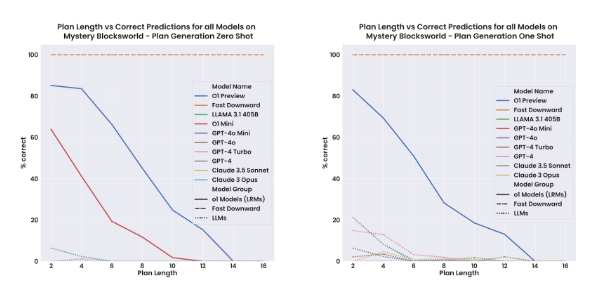
The new model o1 is way better at planning, but still terrible compared to an actual deterministic planning algorithm:
Here is the comparison between the three different worlds: quite remarkable how much worse mystery and randomized mystery are vs. the base Blocksworld.