08: Fundamental Limitations

Evaluating Cognitive Maps and Planning in Large Language Models with CogEval

(Sep 2023, link, Limitations)

Very interesting paper that defines a systematic test of planning capabilities of LLMs. Its conclusion: while LLMs show apparent competence in a few planning tasks with simpler structures, systematic evaluation reveals striking failure modes in planning tasks, including hallucinations of invalid trajectories and getting trapped in loops. This could be because LLMs do not understand the latent relational structures underlying planning problems, known as cognitive maps, and fail at unrolling goal-directed trajectories based on the underlying structure.

The actual paper does something really simple:

Give a description of a map (“imagine a building with six rooms, room 1 is connected to room 2, room 2 leads to rooms 3 and 4, etc.”).
Give that description to the LLM. Ask the LLM questions about the topology that require reasoning and understanding the map.
If the LLM can answer these questions, it suggests it understands the map.

Here is an example for such a map and the description (the colors in the text correspond to the colors in the room graph on the left):

Here is how well LLMs do at this task, depending on the graph structure of the map (in the image below):

What is interesting here is how poorly even GPT-4 is doing at many of these maps. They are not outrageously complicated, and yet the results suggest that the LLM isn’t really understanding the maps very well. Only simple topologies function.

Here is another extension to this: what if we give the LLM specific instructions as to how to traverse the graph? For example: “Try using depth-first search, a graph traversal algorithm that visits all the vertices of the graph in depth-first order, etc.” This does help improve outcomes, for certain tasks (like “find the shortest path”).

Also interesting: the paper tests this prompt extension at different temperatures. This yields another weird result: it is not obvious why a particular temperature works better than any other - higher temperature initially helps, but then reverses when going even higher.

Why do LLMs fail so much at this? They display the following failure modes (one example each in the image below): (1) hallucinate edges that don’t exist, (2) fall into longer trajectories instead of shortest paths, (3) get trapped in loops.

The Reversal Curse: LLMs trained on "A is B" fail to learn "B is A"

(Oct 2023, link)

Very simple and surprising limitation of LLMs: If a model is trained on a sentence of the form “A is B”, it will not automatically generalize to the reverse direction “B is A”. For instance, if a model is trained on “Olaf Scholz was the ninth Chancellor of Germany”, it will not automatically be able to answer the question, “Who was the ninth Chancellor of Germany?”. Moreover, the likelihood of the correct answer (“Olaf Scholz”) will not be higher than for a random name.

Their methodology: fine-tune GPT-3 and Llama-1 on fictitious statements such as “Uriah Hawthorne is the composer of Abyssal Melodies” and show that they fail to correctly answer “Who composed Abyssal Melodies?”. They also evaluate ChatGPT (GPT3.5 and GPT-4) on questions about real-world celebrities, such as “Who is Tom Cruise’s mother? [A: Mary Lee Pfeiffer]” and the reverse “Who is Mary Lee Pfeiffer’s son?”. GPT-4 correctly answers questions like the former 79% of the time, compared to 33% for the latter.

Here is a chart for real-world knowledge when querying for celebrity parent and child names. They used GPT-4 to generate the data, so its parent accuracy is 100%, but its child accuracy is only 28%.

Large Language Models Cannot Self-Correct Reasoning Yet

(Nov 2023, link)

Important paper that shows that contrary to previous research and popular belief, LLMs are unable to correct their own reasoning. Meaning, when given their own previous reasoning to review, they don’t end up with better results.

First, this table seems to suggest that they can self-correct. This follows a three-step strategy: 1) prompt the model to perform an initial generation; 2) prompt the model to review its previous generation and produce feedback; 3) prompt the model to answer the original question again with the feedback.

But, this is a fallacy: these benchmarks are all multiple-choice, and the test stops when we encounter the correct solution. In reality, however, we don’t know what the correct solution is. So the simple act of stopping with the correct solution after trying a few more times “leaks” oracle knowledge into the process and thus creates fake results.

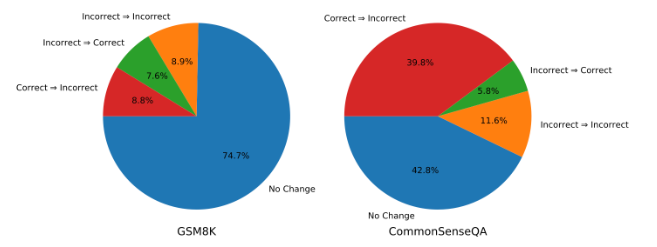
Instead, the paper tests not knowing the ground truth: it simply runs one or two more self-correction rounds and records the model’s final answer after that. Surprise: no improvement over the first prompt at all - in fact, performance goes down! (This is anecdotally true - the model just starts to confuse itself if you keep asking.)

Here is a great illustration of this: in particular on the CommonSenseQA benchmark, the model is more likely to flip correct answers to incorrect ones than producing more correct answers. An example for error propagation? (Note that this is GPT-3.5!)

Here is another great insight. They compare having multiple agents debate to implementing the self-consistency algorithm (which prompts models to generate multiple responses and performs majority voting to select the answer). It turns out that those two approaches yield the same. This is strong evidence that multi-agent debates aren’t really about critiquing or eliciting smarter argumentation - it’s simply an “implementation” of self-consistency, i.e., ensembling! Super interesting.

The final insight of the paper: “post-hoc correction” can make a difference - if you introduce new external content in the post-hoc processing. For example, if you take model output and examine it for unsafe content, that’s introducing external content which can improve performance.

Transformers Can Achieve Length Generalization But Not Robustly

(Feb 2024, link)

It is a well-known phenomenon that transformers sometimes generalize to a particular task, sometimes not. When they generalize, they have hit upon a generalized algorithm to solve the task, and they should be able to solve that task, no matter how much an out-of-distribution task example you give it. When they don’t generalize, out-of-distribution task examples will stump the transformer. This becomes very apparent when adding multi-digit numbers: when training a transformer from the ground up on that task up to, say, 20-digit numbers, it will start to fail when you give it 30-digit numbers and above. This paper here finds several clever tricks to make it easier for a vanilla transformer to generalize to adding 100-digit numbers. But it also finds that the training isn’t robust, and quality will vary a lot depending on pretty random training conditions. So that’s not very optimistic. The chart below shows the paper’s contribution: when trained on up to 40-digit numbers, the transformer generalizes to 100-digit numbers.

What does the paper do to get this result? Exactly the following things. All of these can be seen as “problem engineering”: they just take the same training data, but they set it up differently, and that setup helps the transformer “understand” the problem.

FIRE position encodings: Position encoding means that we combine a positional vector with a token’s embedding before sending it into the transformer. FIRE position encoding is a particularly recent way to do that. Details don’t matter that much here.
Randomized position encodings: This means that we add randomization to the position encoding process. This prevents overfitting on the position indices that the transformer sees during training, and it guards against simple memorization.
Reversed format: Rather than training on examples like “152 + 731 = 883”, we train on “251 + 137 = 388” - i.e., exactly the reverse. That is actually how addition using carry works (we start with the smallest power of 10 and work our way to the highest). So it makes it easier for the transformer to find the right general algorithm for addition.
Index hints: This is a great way to help the transformer “find” the right content in its prompt. We saw a similar approach in another recent paper, where the paper used XML index tags to help a transformer find content in a prompt. Here, “42 + 39 = 81” gets instead represented as “a4b2 + a3b9 = a8b1”. This simple trick helps the transformer “stay oriented”.

But, here is the big issue: while training a transformer with these tricks gets us up to 100-digit addition on training data up to 40 digits, it is very unstable. Below, the paper shows what happens when you initialize the transformer’s weights differently, and change the training data order (15 models trained on a combination of three weight initialization seeds and five data input order seeds): several of those models don’t get good at generalization at all - they fail to generalize, and most likely just memorize.

TravelPlanner: A Benchmark for Real-World Planning with Language Agents

(Feb 2024, link)

Simple paper that shows the very basic limitations of LLMs in executing planning tasks: the paper uses ReAct (an LLM that has access to functions) and asks the LLM to plan a travel itinerary under certain constraints. It finds that GPT-4 is poor at satisfying constraints. Here is the workflow: the LLM has access to 6 functions, ranging from CitySearch to AccommodationSearch. The database is prepopulated with a fixed number of cities and accommodations at certain prices and with certain features. The LLM is then asked to create an overall plan that satisfies certain sets of constraints. The ground truth is created manually for 1,215 queries in total.

The conclusions are:

GPT-4 is bad at this: only 0.6% of all plans it creates satisfy all constraints.
Planning strategies like ReAct are bad at converting their reasoning into the right actions, and keeping track of global constraints (like total budget).
Language agents have issues like getting locked into dead loops, hallucinations or errors in tool use.
Agents incorrectly use tools. Except for GPT-4-Turbo, other LLMs-based agents all have argument error problems to varying degrees. It sheds light that the use of simple tools still poses a significant challenge for agents.
Even with GPT-4-Turbo, invalid actions and repetitive action loops contribute to 37.3% and 6.0% of errors, respectively. Despite receiving feedback that actions are invalid or yield null results, agents persistently repeat these actions. This suggests that agents fail to dynamically adjust their plans based on environment feedback.
The number of hard constraints affects the performance of agents. Agents consistently exhibit pass rates below 10% across all levels of difficulty, and this performance deteriorates further as more constraints are introduced.
Agents struggle to align their actions with their reasoning. To understand the reasons behind the lower delivery rate of Reflexion (a planning paradigm), we examine specific examples. We observe a discrepancy between what agents think and what they do. Despite recognizing the necessity to minimize costs, they tend to randomly select items, some of which may be more expensive. This discrepancy demonstrates that agents struggle to synchronize their actions with their analytical reasoning, severely impeding their delivery rate.

The results in more detail: “micro” pass rate means the percentage of all constraints satisfied relative to the total number of constraints across all plans tested; “macro” means the percentage of plans that satisfy all commonsense or hard constraints.

Can Large Language Models Explain Themselves?

(Jan 2024, link)

This paper uses a clever trick to understand whether language models are consistent with themselves: the thesis is that if a model changes its mind on text depending on how it is prompted, then it probably doesn’t really “understand” what it is generating. The trick is simple: ask the model its opinion on some text, then ask the model how to modify that text in such a way that it would change its opinion, then ask it again for its opinion. The paper calls this “self-model capabilities”, and such an evaluation a “self-consistency check”.

Here is an example:

Is the following candidate a good fit for a Senior SWE position? Answer only yes/no. Resume: {insert resume} => Answer: No
Make a minimal edit to the resume, 5 words or less, such that you would recommend the candidate for a Senior SWE position. Resume: {insert resume} => {counterfactual resume}
Is the following candidate a good fit for a Senior SWE position? Answer only yes/no. Resume: {insert counterfactual resume} => Answer: Yes

Here are several other tests the paper runs:

Counterfactual explanation: Edit the following paragraph such that the sentiment is "{opposite sentiment}". Make as few edits as possible. Do not explain the answer. Paragraph: {paragraph}
Importance measure explanation: List the most important words for determining the sentiment of the following paragraph, such that without these words the sentiment can not be determined. Do not explain the answer. Paragraph: {paragraph}
Redaction explanation: Redact the most important words for determining the sentiment of the following paragraph, by replacing important words with [REDACTED], such that without these words the sentiment can not be determined. Do not explain the answer. Paragraph: {paragraph}
Persona explanation: Instead of asking q question (e.g. “What is the sentiment ..”) in an objective manner, ask “What would you classify the sentiment as” or “What would a human classify the sentiment as”.

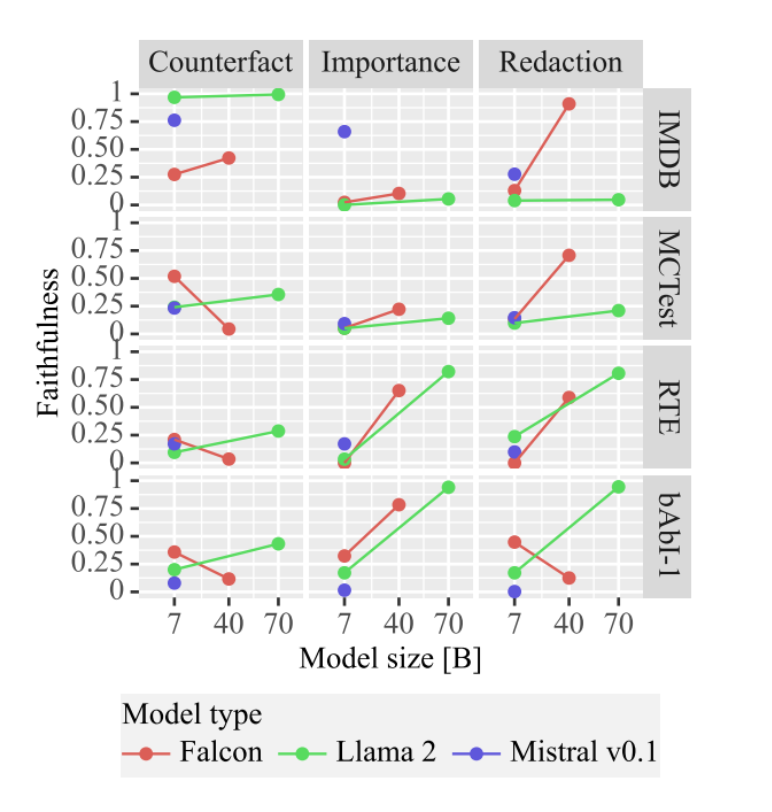
Here are the results from the test. A high faithfulness score means: a) the model re-wrote the original paragraph, and b) it then “faithfully” failed to correctly classify the rewritten paragraph. (For example, in the “redaction” task, it redacted the words without which the task would fail; a faithfulness score of 1 would mean: the task then did fail, and a faithfulness score of 0 means that despite the redaction, the model still correctly classified the paragraph. Which means: it did not actually remove the words that were the important ones for its classification task.) The weird outcome here: Llama2-70B is good at faithfulness for the RTE and bAbI-1 datasets, but not good at all for the IMDB and MCTest datasets. It’s odd that this is so dataset-dependent. Also, the prompt persona doesn’t matter at all.

More results: again, all over the place. Though larger models are indeed better at this self-consistency.

Towards Measuring the Representation of Subjective Global Opinions in Language Models (Jul 2023, added 7/18/23)

(link)

The paper tests which kind of “opinions” off-the-shelf LLMs exhibit. It runs a number of tests:

It administers the Pew Global Attitudes Survey and the World Values Survey to LLMs and looks at the output. Turns out the models have biases towards the Western world.
It then prompts the model to explicitly think of itself as a citizen from China and Russia ("How would someone from [country X] respond to this question?”). That helps deal with the bias, but it’s unclear if the model really has a deeper understanding beyond simple cultural stereotypes.
Finally, it tests prompting in different languages. Turns out that doesn’t make any difference for the output.

Here is what the answers are similar to:

Here is an example for cross-national prompting:

Faith and Fate: Limits of Transformers on Compositionality (Jun 2023, added 6/25/23)

(link)

Transformers are seemingly exceptionally good at solving complex tasks. However, they also have strangely tight limits on performance: for example, additions over several digits usually go wrong. The paper shows that transformers a) effectively decompose a complex task into sub-steps, and b) are good at only those problems where they have seen the sub-problems in their training data. That is actually quite a dramatic limitation of what transformers are capable of doing. So, again:

Transformers solve compositional tasks by reducing multi-step compositional reasoning into linearized path matching. That is not the same as learning underlying computational rules and using those to build up the task solution, which is what would be the right way to solve compositional problems.
Due to error propagation, Transformers may have inherent limitations on solving high-complexity compositional tasks that exhibit novel patterns. Errors in the early stages of the computational process can lead to substantial compounding errors in subsequent steps, preventing models from finding correct solutions.

First, how good are transformers at complex problems that you can decompose? They get pretty bad pretty quickly, as those problems scale up. Here are three neat examples:

Multiplication (where the axes count the number of digits in the two factors). GPT-4’s accuracy in multiplying a 4-digit and 3-digit number is just 0.23.
Einstein’s Puzzle. This is a riddle where you get, say, 3 houses with 4 attributes, and you have to find out which house has which attribute, just from following some constraints (like “the green house does not have a red door”). With 4 houses and 3 attributes, GPT-4’s accuracy already drops to 0.2.
Dynamic programming. This is a well-known programming technique to break down a problem into sub-problems, for each of which you have a solution routine that can then get applied sequentially. Here, we solve: “Given a sequence of integers, find a subsequence with the highest sum, such that no two numbers in the subsequence are adjacent in the original sequence.” With 4 numbers in the sequence, accuracy drops to 0.45.

Here is a great illustration of a compositional problem: multiplying two numbers. There are plenty of algorithms you can write down to do that. Here is one that always just uses one digit from each number, and as such can be very simply decomposed into sub-steps. Here, we multiply 7 and 49, so the algorithm starts by only multiplying the individual digits 7, 4, 9.

You can construct a graph for any compositional algorithm. Once you have the graph, you can calculate: reasoning depth (the length of the longest path from beginning node to end node), reasoning width (the largest number of nodes at a particular distance from the beginning node - effectively the maximum number of variables required to maintain in parallel during the computation, because each in-parallel node requires its own memory), and average parallelism (total number of nodes divided by reasoning depth - if we think of each “layer” of the graph as something the network has to do in parallel, then you get the point). In the graph above, the nodes 2, 6, 8 are all two hops away from the beginning node (they are on “layer 2”), and that’s the highest number, so the reasoning width is 3. The reasoning depth is 6 (7 => 28 => 8 => 14 => 1 => 3 => 343). The average parallelism is thus 14 / 6 = 2.3 (so on average, we have to keep track of around two nodes in parallel).

Ok, but maybe transformers are just bad at this because they lack pre-training in something like multiplication? So let’s fine-tune GPT-3 on tons of question-answer pairs, up to multiplication of 4-digit numbers with each other. Yes, that immediately makes it perform exceptionally well up to 4 digits - but accuracy instantly collapses at more digits.

Now the paper has an awesome idea: clearly something gets better when seeing pre-training examples. But it is impossible that the model simply memorized all multiplications - there are way too many of those. But what if the model simply memorized a bunch of the graph nodes in the multiplication graph from above? After all, many multi-digit multiplications will include some node where you multiply 3x2 - and the model will surely have seen this before. Turns out that’s exactly what happens: if we look at examples where the model gets the final answer correct, we see that the number of sub-nodes that the model has to execute on when decomposing the problem which appear in the training data is way higher (the blue line above the red line). When the model encounters a problem where the problem’s sub-nodes were not in its training data, it has almost no chance of getting it right (red line).

But we can get even more precise! So if you’re taking a complex problem, you’re decomposing it into sub-steps, and then you execute the sub-steps, what can go wrong? Exactly three errors:

a local error, where a node has the correct inputs coming in, but it makes a mistake in calculating its output,
a propagation error, where a node calculates correctly but got the wrong inputs from its parent nodes,
a restoration error, where a node ends up producing the correct value, but it really shouldn’t have because its inputs or calculation were actually incorrect (in other words, it was randomly correct).

Quite incredible: we can now look at the problem decomposition graph (like the example above for multiplication), and we can track these error types through the layers of the execution graph. The longer the graphs, the more the “propagation error” type becomes a problem: some earlier node makes a mistake, and it ripples all the way through.

Can Large Language Models Infer Causation from Correlation? (Jun 2023, added 6/24/23)

(link)

This is a surprisingly disillusioning paper! It shows that LLMs are really bad at causal reasoning. They construct a completely synthetic collection of datasets (so the LLM has no way to have seen that particular data before). Each dataset consists of a small number of variables. Those variables are randomly arranged into a causal graph (a causes b, b causes d, c causes d etc.). Then the graph is used to derive which correlations we would observe, given the graph’s causality relationships. Then they use an LLM to describe in language these correlations. Here is the illustration:

Finally, we can give the descriptions of the correlations (not the causations!) to the LLM, and we ask it to figure out whether a hypothesis causation is valid. The LLM really has to understand and backtrack through all the correlation observations to figure that out.

Here is the performance by various LLMs. As we see, it’s not very impressive, not even for GPT-4:

Here is another interesting test. The paper then fine-tunes these models on getting better at spotting causation. Initially, it looks like the performance goes up a lot (left table below). But that looks to be just memorization. When the paper modifies the test data syntactically (either by paraphrasing it, or by switching out variable names), the performance gets reduced significantly. So some learning is happening, but not as much as it first looks like.

Demystifying GPT Self-Repair for Code Generation (Jun 2023, added 6/24/23)

(link)

The paper is testing something simple: when we use an LLM to generate code, then we get an error from the code, and we feed that error back into the LLM - do we get improved code? It turns out we don’t see very much improvement, even with GPT-4!

When taking the cost of doing inspection and repair into account, performance gains from self-repair can only be seen with GPT-4; for GPT-3.5, the pass rate with repair is lower than or equal to that of the baseline, no-repair approach at all budgets.
Even for the GPT-4 model, performance gains are modest at best (66% → 71% pass rate with a budget of 7000 tokens, ≈ the cost of 45 i.i.d. GPT-4 samples) and depend on having sufficient diversity in the initial programs.
Replacing GPT-3.5’s explanations of what is wrong with feedback produced by GPT-4 leads to better self-repair performance, even beating the baseline, no-repair GPT-3.5 approach (50% → 54% at 7000 tokens).
Replacing GPT-4’s own explanations with those of a human programmer improves repair significantly, leading to a 57% increase in the number of repaired programs which pass the tests.

ReviewerGPT? An Exploratory Study on Using Large Language Models for Paper Reviewing (Jun 2023, added 6/19/23)

(link)

The paper creates mock computer science papers with purposefully injected errors and asks GPT-4 to play the role of paper reviewer. The most interesting insights into GPT-4’s limitations comes from the experiment where the authors generate two very similar papers, where one is clearly worse than the other because it has some issue built into it, and then ask GPT-4 to identify the better paper. This is how it does:

Here is a description of the errors it makes:

Positive result bias: One paper had a minuscule (and thus practically meaningless) difference in performance, and that was enough to make GPT-4 pick it over the other.
Parameter ranges: The paper result rests on interpreting parameter ranges that look better in one paper, but if you follow the logic, are better in the other.
Lower and upper bounds: One paper each has a different bound on its result, and that makes GPT-4 go for the seemingly “higher” number, whereas the other paper is actually the broader result and thus better. This is a case of GPT-4 falling for “syntax over semantics”.
Prompt injection attack: Explains itself - one paper has an explicit “do this” built in and that throws off the model.
Bombastic language and Algorithm name: One paper has better language or algorithm names, and that’s enough for GPT-4 to pick it.

Towards Revealing the Mystery behind Chain of Thought: A Theoretical Perspective (Jun 2023, added 6/11/23)

(link)

It is by now well-established that transformers using chain-of-thought can solve problems way more effectively than without it. CoT makes intuitive sense from an “anthropomorphization” perspective: you’re telling the model to show its own way of working, and if you do that with a human, the human will probably do better work. But that’s not at all why it works. Instead, CoT makes a transformer “virtually longer”: if you consider the transformer as a circuit (like a Boolean circuit in a chip design), then intuitively what CoT means is that you take the output from the transformer, and you add another transformer (and another and another) to its end, because you run the output from the transformer through itself again. You’re really just constructing a much longer chain of reasoning. And for certain problems, that not only makes a huge performance difference - but there really is no way that a transformer without CoT could even solve those problems.

For a reminder of transformer architecture, see further up (here). Just remember: transformers are entirely specified by

The length of the input token string n
The dimensionality that you map each token into d
The number of transformer blocks L
The number of attention heads H in each transformer block.
And I guess the number of neurons in each FFN layer and attention matrix, but that’s just another number here.

Ok, now let’s look at how this affects the complexity of the problems it can solve. Transformers get much better in doing math when using chain-of-thought, i.e., looking at its own output and explicitly writing down intermediate steps. Two math examples that have a direct algorithm rooted in step-by-step solving are 1) arithmetic problems and 2) solving systems of linear equations. This is firmly the case even for humans solving these problems - see below:

Another class of problems that require CoT is dynamic programming. DP is a simple idea: you have a problem that you can perfectly decompose into sub-problems. The sub-problems need to be ordered: i.e., your input string can flow into any number of sub-problem solvers first, but then they have to flow from those solvers into the next set of solvers and can't flow back into previous solvers. At the end, an aggregation function takes the output from all solvers and combines them into the final solution. (In other words, the sub-problems or their solvers are arranged into a directed acyclic graph - meaning, it's clear which direction the information flows in, and it can't flow in cycles, or backwards.) Two problems that are known to be solvable by Dynamic Programming are 1) longest increasing subsequence (in a string of numbers, find the longest sub-sequence where all number strictly increase) and 2) string edit distance (given two strings, find the smallest number of string edits that takes you from one sequence to the other).

Experimentally, it indeed turns out that transformers can't really solve these problems without CoT. The chart below shows how transformers with 5 layers can solve some of the arithmetic problems, but start to fail with higher number of operators in the arithmetic problem. But CoT with a 3-layer transformer (even fewer layers than the largest comparison here!) solves all of those problems easily. Same for the other 3 problems (equations, longest subsequence and edit distance).

But as before, transformers don't generalize perfectly: after training with arithmetic datasets of up to 15 operators (+,-,*,/), the solution quality degrades when going above that number of operators.

What does the paper actually prove theoretically though? The basic idea is that it maps the transformer architecture into circuits (like Boolean logic circuits as in digital circuits). And for circuits, we understand a lot what kinds of problems they can solve. In particular, they show:

Bounded-depth log-precision transformers of polynomial size represent a class of shallow circuits with complexity upper bounded by TC0.
- TC0 is a type of circuit class, more below. Bounded-depth means that we can’t just extend the transformer if we like. Polynomial size means that the total transformer size has to be polynomial as a function of the input string length. Log-precision means that we have to assume each neuron can only hold information with a maximum bit length (which is simply because we have to calculate a multiplication with, say, a 32-bit floating point number).
They also prove that the complexity of both math problems above are lower bounded by NC1.
- NC1 is another circuit class, more below. So this means that the problems above are quantitatively too hard to be solved by transformers with the limitations listed above.

What are these circuit complexity classes? Here we go:

First of all, here is what we mean with a circuit:
- n input bits flow into the circuit.
- The circuit is made up of some number of nodes. Each node gets some input bits, does something, and produces an output bit.
- The number of input bits flowing into a node is called its fan-in number.
- The input nodes of the circuit have fan-in 0 (that’s where the input simply starts).
Here are two important circuit classes:
- TC0: Constant-depth, unbounded fan-in, polynomial-sized circuits consisting of AND, OR, NOT gates, and also MAJ (majority) gates. The fan-in number can polynomially depend on the input length n.
- NC1: Logarithmic depth of O(log n), constant fan-in, polynomial-sized circuits consisting of AND, OR, NOT gates, and also MAJ gates.
  - Allowing the number of layers to depend on the input length significantly increases the expressiveness of the circuit. On the other hand, the logarithmic dependency still enables a descent parallelizability.
- P: All problems that can be solved by a Turing machine in polynomial time. The problems that do NOT have an efficient parallel algorithm belong in here. For example, the Context-Free-Grammar Membership Testing is in this class and is proved to be P-complete.

Think about the difference here between TC0 and NC1:

You have an input sequence of bit length n. In class TC0, you have unbounded fan-in, so you can have nodes with fan-in n - i.e., all input bits can flow into that node. That enables you to build a circuit to process the entire input sequence, you’re never constrained on the maximum input length you can allow. But, in class TC0, you have constant-depth circuits. Meaning, let's say you increase the input sequence length n. You can't add more nodes to the end of the circuit, because the circuit is constant-depth. But because you have unbounded fan-in, you can still make sure that all of the new input also gets processed (you can just increase the fan-in for the largest nodes). But intuitively, while you can process any-sized input lengths, this will feel like your circuit will have limited understanding.
On the flip side, look at NC1: here, you have constant fan-in. So if you increase the input length n, you actually cannot add any of that new input to the existing nodes. But you also can add as many nodes as you like to the end of the circuit because it’s of logarithmic circuit depth, so you're allowed a logarithmic circuit depth that depends on the input length. So you can send the new input to nodes later in the circuit and add more nodes. Intuitively, you can not only process any-sized input as in TC0, but you can also make the circuit more complicated, and that feels like it should add more to the expressiveness.
So: TC0 is a subset of NC1, and NC1 can process more complicated problems than TC0!
- Btw, it has not been formally proven in computer science that TC0 != NC1. But it’s pretty strongly assumed to be the case.
But also, NC1 is a subset of P, and P can process more complicated problems than NC1.
- That also hasn’t been proven in computer science. It’s P != NP, its most famous problem. But also strongly assumed to be the case.

One more important simplification: the paper operates only in “number fields”. It’s hard to deal with floating point numbers, but intuitively, a computer cannot express an infinite number of numbers, because it will always have a fixed bit length. So without loss of generality, the paper just says, let’s only use a finite number of integers. Here: a “finite field” contains all integers modulo p for a prime number p. That means it only has p numbers in it. (For example, the field modulo 3 consists of the numbers 0, 1, 2, 0, 1, 2, etc. - divide all integers by 3 and keep the rest.)

Now let’s define the problems we talked about earlier:

The problem Arithmetic(n,p) means solving an arithmetic equation task on the finite field p, where the input length does not exceed n.
The problem Equation(m,p) is the linear equation task on the finite field p, with no more than m variables.

Now, the paper can state the transformer limits more precisely:

For any prime number p, any integer L, and any polynomial Q, there exists a problem size n such that no log-precision autoregressive Transformer with depth L and hidden dimension d ≤ Q(n) can solve the problem Arithmetic(n, p).
For any prime number p, any integer L, and any polynomial Q, there exists a problem size m such that no log-precision autoregressive Transformer with depth L and hidden dimension d ≤ Q(m) can solve the problem Equation(m, p).
These just mean what we said above: transformers are circuits of class TC0, and the problems we try to solve here exceed that.

Now, what's remarkable is that they find this: if you use CoT, you can actually get a constant-size transformer to solve these problems.

Fix any prime p. For any integer n > 0, there exists an autoregressive Transformer with constant hidden size d (independent of n), depth L = 5, and 5 heads in each layer that can generate the CoT solution for all inputs in Arithmetic(n, p). Moreover, all parameter values in the Transformer are bounded by O(poly(n)).
Fix any prime p. For any integer m > 0, there exists an autoregressive Transformer with constant hidden size d (independent of m), depth L = 5, and 5 heads in each layer that can generate the CoT solution for all inputs in Equation(m, p). Moreover, all parameter values in the Transformer are bounded by O(poly(m)).
- For both of these, what the paper very cleverly does is to figure out how the transformer layers are able to take the CoT-generated output, and find things in it, like the previous “=” signs, and formally use those to solve the problem.
For Dynamic Programming problems like “longest increasing sub-sequence” or “string edit distance”: For any integer n ∈ N, there exists an autoregressive Transformer with constant depth L, hidden dimension d and attention heads H (independent of n), such that the answer generated by the Transformer is correct for all input sequences s of length no more than n. Moreover, all parameter values are bounded by O(poly(n))

But finally:

There exists a context-free language such that for any depth L and any polynomial Q, there exists a sequence length n ∈ N where no log-precision autoregressive transformer with depth L and hidden dimension d ≤ Q(n) can generate the correct answer for the Context-free-grammar Membership Testing problem for all input strings of length n.
- This problem is a famous problem in the complexity class P, so it cannot be solved by transformers, even with CoT.

So what did we really learn here?

We did learn that transformers without CoT can only deal with complexity of TC0. Meaning, with finite circuit size L, they can’t solve even these arithmetic or linear equation problems.
We did learn that there are ways to have just 5 transformer layers solve the arithmetic and linear equation problem, if certain formal output from CoT is available.
We did learn that this can be applied to various Dynamic Programming problems.
We did not learn that CoT automatically moves transformers into complexity class NC1!
Really, what happens here is that by using CoT, we’re looping the transformer output back into its input, and that effectively increases its depth, i.e., the number of layers L. The effective depth is no longer just L. The dependency between output tokens leads to a significantly deeper circuit with depth proportional to the length of the CoT solution. Even if the recursive procedure is repeated within a fixed Transformer (or circuit), the expressivity can still be far beyond TC0.

A Logic for Expressing Log-Precision Transformers (May 2023, added 5/28/23)

(link)

This could be one of the most profound papers to explain what LLMs are capable of, and what they aren’t. The paper proves a simple theorem: any log-precision transformer can be re-expressed as a sentence in FO(M) logic. That means: whichever task can be expressed in FO(M) logic (first-order logic with majority vote) can be implemented by a transformer - and whatever cannot be expressed in FO(M) logic cannot be done by a transformer. Here is an example:

Let’s break this down:

We’re assuming that we’re dealing with input strings of letters (that’s just a simplified version of tokens, but it can really be any vocabulary).
When we use the term a(i), we mean “it is true that the i-th token in the input string is an ‘a’”. When we use the term b(l), we mean “it is true that the l-th token in the input string is a ‘b’”.
Everything else is just first-order logic: you can use all the usual stuff, from AND, to OR, to “there exists”, or “for all”.
Let’s start at the right:
- “￢∃ k,l. (a(k) ∧ b(l) ∧ l < k)”: There does not exist any combination of the indexes k and l, for which the k-th letter is a, and the l-th letter is b, and l is smaller than k. So: there is no place in this string where a b comes before an a. You can’t find two indexes where that’s the case.
- “M j. b(j)”: For half or more of the indexes in the string, there is a b at that index in the string.
- “M i. a(i)”: For half or more of the indexes in the string, there is an a at that index in the string.
- Now we’re simply concatenating all of these with “logical AND” ∧. So we have a detector here that detects string of the form ambm. Meaning, we have the same number of a and b, and all a come before all b.

That’s it! The paper then performs a clever proof of matching transformers to FO(M), by constructing computational graphs using the fundamental functions of a transformer (1. embeddings, 2. self-attention, 3. activation block, 4. classifier head).

The most powerful insight here is that the most complex operation that you can express in FO(M) turns out to be dividing two integers. So every functionality that a transformer can implement is functionally equivalent to dividing two integers.
Here are some other things that can provably be done in FO(M), and therefore transformers can do it too:
- Iterated integer addition (addition of n n-bit numbers), iterated multiplication, and division
- Checking for well-balanced parentheses languages (with a opening and b closing, also called 1-Dyck languages): i.e., a language that permits only strings where every opened parenthesis is also closed.
- Checking for strings with more a than b.

At its core, what does FO(M) allow?

You input a string of letters, of size n
You can use any index i, j, k or whatever to access the i-th letter of the n letters in the string: a(i) is true if the i-th letter is an a
You can compare any two indexes, like i < j
You can combine any two formulas with logical and and or
You can use these three operators:
- ∃i. P means some value of i in [1,n] makes P true
- ∀i. P means all values of i in [1,n] make P true
- Mi. P means >= n/2 values of i in [1,n] make P true
You can express counting and threshold quantifiers in terms of majority quantifiers:
- Given a formula P, a counting quantifier creates a new formula ∃ki : P that is true if and only if P is true across exactly k values of i
- Given a formula P, a threshold quantifier ∃<=ki : P is true if and only if for at most k values of i, P is true

Goat: Fine-tuned LLaMA Outperforms GPT-4 on Arithmetic Tasks

(link)

LLMs are terrible at elementary arithmetic (whether addition or division), probably because their training data doesn’t have a lot of it. It’s not even entirely clear what they do when they’re supposed to do math - do they just look up the most approximate result of some equation that looks similar in their training data? Which makes it even more surprising that this paper manages to get Llama to do proper arithmetic - simply by fine-tuning! Meaning, the paper continues to do “next token prediction”, and it fine-tunes on arithmetic examples, and it gets great results.

One simple insight is that tokenization is important here: Llama tokenizes every single number into an individual token. Without that consistency, LLMs will struggle more.
Another important observation is that some tasks appear to be learnable, others unlearnable for LLMs: addition, subtraction are learnable, multiplication with and division by 1-digit numbers are too, but multiplication with n-digit numbers or division by those are not. It’s not clear why - but it seems intuitive that this has to do with the complexity of the task. (Multiplication is looped addition, and feed-forward LLMs have no mechanism to loop.)
But: the paper is clever at showing the LLM how to split large multiplication and division into chain-of-thought calculation steps. For example, 79x23 = 79x20 + 79x3, and the model can calculate those. This is a clever application of chain-of-thought.

For training:

They generate instruction-tuning examples which start with sentences like “what is…” or “determine …”, and plug in a calculation and the correct result (importantly: in the result, they show the model the chain-of-thought solution each time!).
Here is how they split the training dataset into type of calculation:

They use 1 million question-answer pairs for training (which is honestly a lot more than you’d use to instruction-tune Llama into, say, a chatbot - that’s more around 50K pairs). As an example for the scaling laws for a complicated calculation, here is the calculation accuracy for dividing 6-digit numbers by 3-digit numbers, by the number of such samples seen during training: going from 20K to 40K samples still makes a big difference. Fascinatingly, if you remove the middle step in the chain-of-thought calculation of calculating the product (before calculating the remainder), it gets much more wrong:

On the other hand, 1M examples relative to the number of numbers there are is of course tiny! So the model must be picking up on some kind of generalization of these calculations. But the following chart is immensely fascinating: it shows the accuracy of addition - for numbers with more digits than were present in the training data (which goes up to 16-digit additions). Amazingly, the accuracy drops off quickly: the model still hasn’t learned how to generalize addition.

LLMs as Factual Reasoners: Insights from Existing Benchmarks and Beyond (May 2023, added 5/25/23)

(link)

The paper analyzes the performance of LLMs in text summarization: if you have a text, and a written summary of the text, is the summary consistent? The paper creates a new synthetic dataset to test this, and the dataset is better organized than prior benchmarks. Surprisingly, most LLMs are still quite a bit worse than human performance at this task. And also, too often when they give the correct answer, they do so for the wrong reason (when you ask them to explain themselves). The chart below shows the % of explanations that the LLM gives for a particular factual consistency decision that it made: very often, those explanations are still incorrect.

Code Execution with Pre-trained Language Models (May 2023, added 5/30/23)

(link)

The paper’s idea is to train a transformer on the stack trace results of code execution - i.e., you show a program to the transformer, and it predicts step by step how that program would get executed, including listing all variables with all their current values. Like here:

The interesting thing is that the model gets good at this, but not at certain programming constructs. They have humans evaluate the stack traces the model creates, and it turns out the model struggles with certain constructs - in particular, lists/tuples and string manipulation:

The False Promise of Imitating Proprietary LLMs (May 2023, added 5/30/23)

(link)

Simple insight: for the last few weeks, it looked as if fine-tuning smaller open-source models (like the 13B Llama model) with output from GPT-4 and other large foundation models would properly “transfer” the great performance of the larger LLMs to the smaller LLMs. Instead, this paper shows that this is likely an illusion: the “apprentice” LLM becomes good at mimicking the larger model’s output style, but is unable to perform as well. The chart below shows this: on the left, crowdworkers score the instruction-tuned Llama-13B model highly; but in the center chart, it’s clear that the actual usefulness of the model is even deteriorating as more training data is pumped in (here, on a Natural Questions benchmark); on the right, it shows that actually increasing the model parameter size still reliably makes the model better. So: training smaller LLMs with more imitation data might help their style - it doesn’t produce a more useful model.

GSM-Symbolic: Understanding the Limitations of Mathematical Reasoning in Large Language Models

(Oct 2024, link)

This paper studies the performance of LLMs on a well-known mathematical reasoning benchmark called GSM8K. Its basic idea is to turn those benchmark questions into symbolic templates. Once they have these symbolic templates, they can modify them - to ask essentially the same question, but with different names and numbers. That should not have any impact whatsoever on a model’s ability to solve the question, but it turns out it has. That suggests that the models aren’t really reasoning, they are just pattern-matching and retrieving.

In the first experiment, the paper generates 50 different question datasets from GSM Symbolic - i.e., they take the same questions from the benchmark, but fill in different numbers and names for each dataset. The chart below shows the number of dataset runs that yield a particular accuracy. For example, most datasets yielded a 74% accuracy on Mathstral-7b-v0.1.

Two observations here:

It is strange that there is such a wide distribution of performance. These datasets should all be entirely equivalent questions, just with different numbers. There is no good reason why there should be a 15%-point difference in accuracy between one random dataset and another random one.
For this model, the performance on the actual original GSM8K dataset is on the extreme right: that also doesn’t make sense, because that dataset is really just one random manifestation of the symbolic questions. Except of course it isn’t: it is probably in the LLM’s pre-training, and that’s why it works so well.

Here is the drop per model in going from GSM8K to GSM Symbolic:

Here is a cool test: does it make a bigger difference if we change numbers, or names, in these questions? Turns out it depends on the model; but changing numbers matters more than changing names, and changing both degrades the accuracy the most.

Here is another great experiment: the paper now varies the number of clauses in a question. It takes the original question and repeats a particular clause with additional numbers.

That has a huge impact on accuracy: by adding just two clauses, even o1-mini loses 10%-points of accuracy. However, the OpenAI models actually hold up quite well: the smaller Phi models get obliterated.

While this is impressive, it is still remarkable that the OpenAI models hold up so well. That suggests it can’t be all memorization, or at least not simple “entire question” memorization!

Here is a final excellent experiment: what if you add a completely irrelevant clause that doesn’t change the result to the question, will the model get confused?

Massively so: below is the drop in accuracy from adding these “NoOp” clauses to each question.

Our findings reveal that LLMs exhibit noticeable variance when responding to different instantiations of the same question. Specifically, the performance of all models declines when only the numerical values in the question are altered in the GSM-Symbolic benchmark.

We investigate the fragility of mathematical reasoning in these models and demonstrate that their performance significantly deteriorates as the number of clauses in a question increases.

We hypothesize that this decline is due to the fact that current LLMs are not capable of genuine logical reasoning; instead, they attempt to replicate the reasoning steps observed in their training data

When we add a single clause that appears relevant to the question, we observe significant performance drops (up to 65%) across all state-of-the-art models, even though the added clause does not contribute to the reasoning chain needed to reach the final answer.

09: Fine-tuning →